100 Problemas por José Paulo Viana

Por motivos que, julgo, facilmente compreenderão, no 100 Problemas deste mês gostava de partilhar convosco parte de um texto publicado no meu livro “Uma Vida Sem Problemas” (Edição Clube do Autor, 2012). 

Se dois triângulos são geometricamente iguais, então têm obrigatoriamente seis elementos iguais: os três lados de um são iguais aos três lados do outro, e o mesmo acontece com os três ângulos.

A Ana Rita afirmou:

– Desenhei dois triângulos diferentes, embora tenham cinco elementos iguais.

Será possível?

Dos problemas que me apareceram nos últimos tempos, este foi o que mais me entusiasmou. Encontrei-o na revista francesa Tangente nº 114, com a indicação que aparecia no livro O Circo Matemático, de Martin Gardner.

Quando lemos o enunciado, parece-nos impossível que tal possa acontecer: cinco elementos iguais de um triângulo para o outro e eles são diferentes? Mas, por outro lado, se o problema nos é apresentado, é porque tem solução. E é esta tensão entre a nossa intuição (que nos diz que é “impossível”) e a nossa razão (que. nos diz que, se ele ali está, é porque deve ser possível) que nos faz querer descobri a solução.

E a Ana Rita tem razão. Existem realmente triângulos em que, de um para o outro, cinco dos seis elementos são iguais.

Então, antes de continuar a ler, não quer o leitor tentar descobrir um destes triângulos? Vale a pena!

Vejamos qual pode ser o elemento diferente.

Poderá ser um ângulo? Isso significaria que um triângulo teria ângulos a medirem A, B e C, e os ângulos do outro mediriam A, B e D. Mas, como a soma dos ângulos de um triângulo é 180º, teríamos:

A + B + C = A + B + D = 180º  e portanto  C = D.

Outra maneira de raciocinar era que, se o elemento diferente fosse um ângulo, então os três lados de um triângulo seriam iguais aos lados do outro. Mas dois triângulos nestas condições são geometricamente iguais (é o caso mais simples de igualdade de triângulos) e portanto os três ângulos de um seriam iguais aos do outro. Impossível.

Conclusão: o elemento diferente é um lado.

Como os três ângulos são iguais, os dois triângulos são semelhantes (têm a mesma forma).

Quando existe uma semelhança, se dividirmos os lados correspondentes das duas figuras obtemos sempre o mesmo resultado, que se chama razão de semelhança.

Se os lados do triângulo maior medirem, por ordem crescente, A, B e C e os do menor medirem a, b e c, teremos:

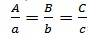
é igual a  k (razão de semelhança).

Daqui resulta  A = k.a;  B = k.b; C = k.c

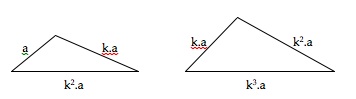
Como os triângulos têm tamanhos diferentes, os lados que são iguais não são do mesmo tipo. O lado intermédio do 1º triângulo terá de ser igual ao menor do 2º; o lado maior do 1º será igual ao lado intermédio do 2º. Ou seja, temos de arranjar maneira de fazer com que:

b = A = k.a
c = B = k.b = k².a