100 Problemas com José Paulo Viana
Clube de Matemática SPM - Eixos de Opinião julho de 2015

Ah, os problemas!
Lembram-se do prazer que é encontrar um problema, daqueles que nos desafiam logo que o lemos, e depois avançar na resolução até conseguir descobrir a resposta?
Recordam-se da alegria que é descobrir a forma elegante e simples que alguém encontrou para resolver um problema que julgámos impossível ou que tanto trabalho nos deu?
E, finalmente, concordam que entusiasma discutir com outras pessoas a maneira de chegar à solução de um problema que nos intriga?
Pois é por estes três motivos que esta secção existe.
José Paulo Viana - Professor de Matemática na Escola Secundária de Vergílio Ferreira, autor da seção "Desafios" aos domingos no jornal Público

Ah, os problemas!
Lembram-se do prazer que é encontrar um problema, daqueles que nos desafiam logo que o lemos, e depois avançar na resolução até conseguir descobrir a resposta?
Recordam-se da alegria que é descobrir a forma elegante e simples que alguém encontrou para resolver um problema que julgámos impossível ou que tanto trabalho nos deu?
E, finalmente, concordam que entusiasma discutir com outras pessoas a maneira de chegar à solução de um problema que nos intriga?
Pois é por estes três motivos que esta secção existe.
José Paulo Viana - Professor de Matemática na Escola Secundária de Vergílio Ferreira, autor da seção "Desafios" aos domingos no jornal Público
100 Problemas com José Paulo Viana - O triângulo das Mediatrizes...
Clube de Matemática SPM - Eixos de Opinião julho de 2015
Clube de Matemática SPM
Título: O Triângulo das Mediatrizes
Será possível descobrir um triângulo tal que estas três retas, concorrentes no ponto O, sejam as mediatrizes dos seus lados?

O aparecimento dos programas de geometria dinâmica nos computadores e nas máquinas de calcular tornou a resolução deste tipo de problemas numa atividade de investigação e descoberta quase sempre interessante e empolgante. Acabamos muitas vezes por encontrar relações insuspeitas entre os vários elementos geométricos.
O nosso conselho, caro leitor, é que, antes de continuar a leitura deste artigo, abra um destes programas no seu computador e tente resolver o problema. É muito provável que descubra um método interessante de chegar à solução, bem diferente daquele que aqui vamos mostrar.
Antes de avançarmos, é preciso notar que, se encontrarmos um triângulo para estas mediatrizes, todos os triângulos que se obtiverem a partir deste, por uma homotetia de centro O, serão também soluções do problema.
Consideremos uma reta u, perpendicular a r, sobre a qual irá estar um dos lados do triângulo. Marquemos nessa reta um ponto A, eventual vértice do triângulo procurado. Como r é a mediatriz de um lado, se fizermos a reflexão de A em relação a r, iremos obter um novo vértice B.
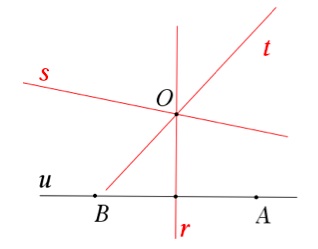
Por sua vez, a reflexão de B em relação à mediatriz s irá dar o terceiro vértice C. Finalmente, a reflexão de C em relação a t dá um ponto A’, que deveria coincidir com o vértice A.
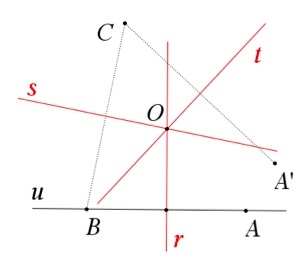
Como A e A’ não coincidem, isso quer dizer que a posição inicial que escolhemos para A não corresponde a uma solução. Agora, poderíamos deslocar o ponto A ao longo de u, até que A e A’ coincidissem. Mas essa coincidência nunca seria perfeita e iríamos obter apenas uma aproximação da solução. (Nota: outra hipótese era deslocar a reta u, mantendo A sempre à mesma distância de r, mas a questão da coincidência imperfeita mantinha-se.)
No entanto, se continuarmos a fazer experiências, é bem possível que encontremos relações insuspeitas. Uma delas é que todas as soluções irão ter aquele vértice, a que chamámos inicial, na mediatriz do segmento AA’.
Está então encontrado um método “simpático” para obter uma solução. Basta traçar essa nova mediatriz de AA’ e procurar o seu ponto P de interseção com u.
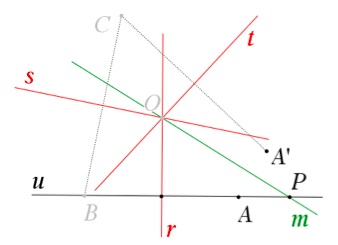
Agora, por reflexões sucessivas de P em relação a r e a s determinam-se os outros vértices do triângulo PQR e o problema fica resolvido