(U)Ma Temática Elementar por José C. Santos
Clube de Matemática SPM - Eixos de Opinião setembro de 2016
|
|
José Carlos Santos - Departamento de Matemática da FCUP Dia 21 de cada mês
|
(U)Ma Temática Elementar por José Carlos Santos - Vendo somas
Clube de Matemática SPM - Eixos de Opinião setembro de 2016
Clube de Matemática SPM
Facebook Clube SPMTítulo: Vendo somas
Neste texto, iremos abordar um tópico que tem pontos em comum com o que foi abordado no texto sobre Geometria e Álgebra: como calcular certas somas geometricamente. Por exemplo, qual é o resultado de se somarem os n primeiros números naturais (1 + 2 + … + n)? A resposta é n×(n + 1)/2. Vejamos como é possível uma pessoa convencer-se disso com figuras. Uma maneira de visualizarmos a soma dos 4 primeiros números naturais é a seguinte:

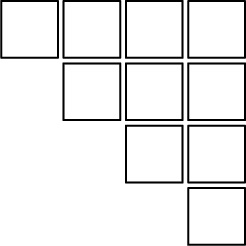

2x(1 + 2 + 3 + 4) = 4x5.
Mas o que foi feito aqui com o número 4 funciona com qualquer número, pelo que
2x(1 + 2 + ... + n) = nx(n + 1).
Aliás, o que foi feito aqui não exige que se comece com o número 1. Por exemplo, quanto é 3 + 4 + 5 + 6 + 7? Pelo mesmo motivo, é metade do número de quadrados da seguinte figura:

Vejamos outro problema semelhante: quanto dá a soma dos primeiros números naturais ímpares? Este problema pode ser abordado de uma maneira semelhante à anterior, mas vamos ver outro método. Uma maneira de visualizarmos 1 + 3 é a seguinte:



Prosseguindo deste modo, fica bastante claro que a soma dos n primeiros números naturais ímpares é n2.
Para terminar, vejamos como ilustrar o facto de a soma dos n primeiros cubos ser igual ao quadrado da soma dos n primeiros números, ou seja que
13 + 23 + … + n3 = (1 + 2 + … + n)2
Para começar, 13 = 1. Quanto a 23, vamos encará-lo como 2×22. Geometricamente, vamos ver isto como dois quadrados com duas unidades de lado. Desses dois quadrados, partimos um a meio. Juntando isto a um quadrado com uma unidade de lado, obtemos: