Se e Só Se por José Carlos Pereira
Clube de Matemática SPM - Eixos de Opinião dezembro de 2016
|
|
Nesta coluna pretendo partilhar todos os meses a minha opinião sobre questões relacionadas com a Matemática e com o seu ensino. Os leitores são convidados a comentar, com argumentos a favor ou contra, aliás é esse o objectivo desta coluna: discutir diferentes pontos de vista sobre o tema do artigo (dia 3 de cada mês).
José Carlos da Silva Pereira – Professor de Matemática, autor de livros escolares e responsável pelos sites Recursos para Matemática e MathSucess. Ler artigos anteriores aqui. |
Clube de Matemática SPM - Eixos de Opinião dezembro de 2016
Clube de Matemática SPM
Facebook Clube SPM
Título: Uma Resposta Surpreendente
Já não é a primeira vez que escrevo sobre respostas surpreendentes dadas por alunos. A que trago aqui não se passou comigo, mas com uma colega que a partilhou no grupo do Facebook Recursos para Matemática. Com a devida autorização, começo por reproduzir a primeira parte da publicação que foi feita. Mais adiante reproduzi-la-ei toda:

A resposta esperada a um exercício deste tipo, ou pelo menos a desejada, deverá seguir grosso modo os seguintes tópicos: se P(A∩B) = 3/10 e P(B|A) = 3/4, então, como P(A∩B) = P(A)×P(B|A), vem P(A) = 2/5; por outro lado sabe-se que P(AUB) = P(A) + P (B) − P (A∩B), de onde 1/2 = 2/5 + P (B) – 3/10, pelo que P(B) = 2/5, concluindo-se assim que os acontecimentos A e B são equiprováveis.
No entanto, um dos alunos desta colega não seguiu este caminho, nem outro, digamos, mais convencional, por exemplo, elaborando uma tabela de contingência. A sua resposta está espelhada na imagem seguinte:
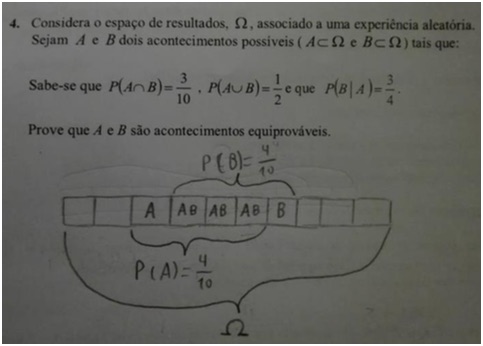
Esta imagem acompanhava a pergunta: “O que me dizem sobre esta resposta de um aluno? É considerada válida?”
O que mais me interessou foi tentar perceber o raciocínio do aluno. Qual terá sido? É um exercício difícil, mas poderá ter sido mais ou menos este: como P(A∩B) = 3/10, o aluno imaginou um espaço dividido em dez partes e preencheu três delas com AB, isto é, com A∩B; depois como P(AUB) = 1/2, teria de preencher mais duas partes, que poderia ser feito de três formas, preenchendo duas com A, ou duas com B ou uma com A e outra com B. No entanto também se tem P(B|A) = 3/4 de onde terá concluído que teria de preencher uma com A e outra com o B, pois caso preenchesse duas com A, ter-se-ia P(B|A) = 3/5 e caso preenchesse duas com B, ter-se-ia P(B|A) = 1; finalmente concluiu o pretendido.
Na discussão que se gerou, surgiram algumas questões em relação a uma suposta falta de rigor e de formalidade da resposta. Não obstante, quase todos os que intervieram destacaram a forma criativa e surpreendente como o aluno abordou a pergunta, considerando a sua resposta correcta.
O que o aluno fez foi exactamente o que nós, professores, pretendemos que um aluno faça quando colocado perante um problema: que o entenda, que trace uma estratégia para o resolver, que aplique essa estratégia e que chegue à solução. O aluno fez isso tudo. Será então legítimo considerar esta resposta incorrecta? Em meu entender não! E no Exame Nacional, como seria classificada? Não sei, mas sei que seria alvo de (uma boa) discussão.
Caso esta fosse uma pergunta de selecção, o aluno, com esta abordagem, acertaria em cheio.
Há respostas que nos surpreendem e esta, é uma delas!
E o leitor, qual é a sua opinião em relação a esta resposta? Deixe o seu o comentário na página do Facebook do Clube SPM.


