Se e Só Se por José Carlos Pereira
Clube de Matemática SPM - Eixos de Opinião março de 2017
|
|
Nesta coluna pretendo partilhar todos os meses a minha opinião sobre questões relacionadas com a Matemática e com o seu ensino. Os leitores são convidados a comentar, com argumentos a favor ou contra, aliás é esse o objectivo desta coluna: discutir diferentes pontos de vista sobre o tema do artigo (dia 3 de cada mês).
José Carlos da Silva Pereira – Professor de Matemática, autor de livros escolares e responsável pelo site Recursos para Matemática. Ler artigos anteriores aqui. |
Clube de Matemática SPM - Eixos de Opinião março de 2017
Clube de Matemática SPM
Facebook Clube SPM
Esta é a segunda vez que faço a reedição de um texto no “Se e Só Se”. Justifica-se pelos factos de nesta altura do ano se começar a abordar no 11.º ano a “nova” definição de limite segundo Heine e de já ter sido várias vezes contactado para esclarecer algumas questões sobre a mesma.
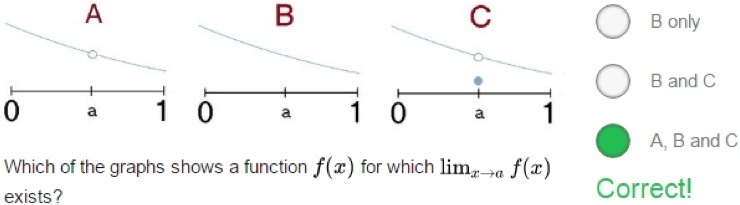
A figura que inicia este artigo foi recortada do site brilliant.org, que já referi neste meu outro artigo. Agora não tanto, mas há uns meses respondia diariamente a uma ou duas questões que por lá iam aparecendo, e esta foi uma delas. Na altura escolhi a última opção quase automaticamente e prossegui com os meus afazeres.
Mais tarde relembrei-me deste problema e voltei à página para ler alguns comentários e observar a tendência dos mesmos. Pude constatar que a grande maioria considerava que nas funções representadas nos “gráficos” das opções A, B e C o limite da função f no ponto a existia. No entanto, para alguns dos que comentaram, esse limite só existe nas funções representadas nos “gráficos” das opções A e B.
Na verdade, uma resposta correcta também é “apenas A e B”: é tudo uma questão de definição!
A resposta “apenas A e B” está correcta à luz da Definição de Limite Segundo Heine do novo Programa de Matemática A do Ensino Secundário, que está actualmente em vigor nos 10.º e 11.º anos e que será estendido ao 12.º no próximo ano lectivo. Foi por causa dela que tive a curiosidade de voltar à página! Essa definição pode ser consultada aqui – página 36 do documento das Metas Curriculares e duas das suas consequências são as seguintes:


Resumindo, se f é uma função real de variável real e a um ponto aderente ao seu domínio, no caso de a ∉ Df é suficiente que os limites laterais sejam iguais (caso existam) para se afirmar que existe limite de f no ponto a. Já se a ∈ Df , não é suficiente que os limites laterais sejam iguais (caso existam) para se poder afirmar que existe limite de f no ponto a, além disso é necessário que sejam ambos iguais a f (a), isto é, f tem de ser contínua no ponto a!
Assim sendo, tendo em conta esta definição, a função cujo “gráfico” está representado na opção C não tem limite no ponto a, pois apesar de os limites laterais no ponto a serem iguais, não são iguais a f (a).
Outro exemplo. Se consideramos a função g de domínio
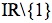
definida por:
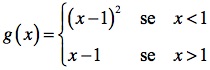
1 é um ponto aderente ao domínio de g e
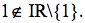
É fácil verificar que o limite de g à esquerda e à direita do ponto 1 é 0, pelo que o limite da função g no ponto 1 existe e é igual a 0. No entanto, alterando ligeiramente a função g de modo a 1 pertencer ao seu domínio, definindo-a em IR, por exemplo, da seguinte forma:
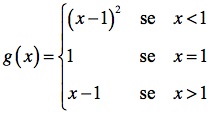

Para o Brilliant, que tem milhões de utilizadores de quase todos pontos do globo, a resposta correcta é a assinalada a verde. Note-se que a resposta não foi contestada por nenhum dos que comentaram! Para eles e para os responsáveis do site a definição de limite é a usada no Programa de Matemática A do Ensino Secundário que ainda se encontra em vigor nos 12.º anos e não outra. Em Portugal, para os alunos que estão a frequentar o 11.º ano, a resposta correcta é a terceira: “nenhum existe”. Já para os alunos que estão a frequentar o 12.º ano, a resposta correcta é a assinalada a verde. Mais uma vez, é só uma questão de definição!
Como fiz na primeira versão deste texto, volto a realçar que em termos práticos nada irá mudar no cálculo de limites. As conclusões é que serão, em alguns casos, diferentes daquelas a que estamos habituados, como o leitor pôde verificar no exemplo anterior. É natural que nestes primeiros tempos esta “nova” definição crie alguma confusão, mas é com ela que temos de trabalhar e é a ela que temos de nos habituar. Esse processo de habituação será ele também natural.
Convido o leitor a deixar o seu comentário sobre este artigo na página do Facebook do Clube SPM.


