100 Problemas por José Paulo Viana
Clube de Matemática SPM - Eixos de Opinião março de 2017

100 Problemas por José Paulo Viana - Um ponto no triângulo
Clube de Matemática SPM - Eixos de Opinião março de 2017
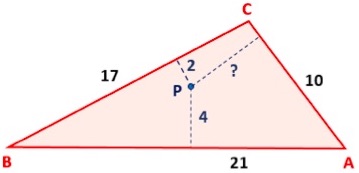

Um dos aspetos de que gosto neste problema é que, quando se começa a pensar nele, nem se sabe bem por onde avançar (pelo menos, foi o que aconteceu comigo…). Parece que a única via é fazer cálculos fastidiosos com quadriláteros e triângulos não retângulos.
No entanto, existe uma resolução muito simples, desde que se conheça a área do triângulo ABC. Não sabemos nenhuma das suas alturas mas, como vimos na edição anterior desta secção (http://www.clube.spm.pt/arquivo/5052), existe a fórmula de Heron para a área de um triângulo, conhecidos os seus lados a, b e c. Se s for o semiperímetro, ou seja, s=1/2 (a+b+c), será
![]()
Tracemos os segmentos PA, PB e PC, que dividem o triângulo inicial em três triângulos.
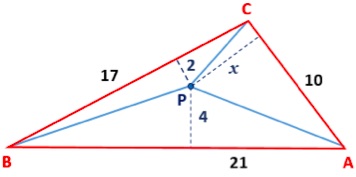
As suas áreas são:
O ponto P está a 5 centímetros do lado CA.
Fácil, não é?


