100 Problemas por José Paulo Viana

100 Problemas por José Paulo Viana - Duas Investigações com Triângulos e Retângulos

1ª INVESTIGAÇÃO

Dado um triângulo qualquer, que admitimos ter uma unidade de área, qual será a área do menor retângulo capaz de o “tapar” (isto é, dentro do qual possamos colocar o triângulo)?

Dado um retângulo de medidas 1x4 unidades, qual será a área do menor triângulo capaz de o “tapar”?

Leitor, antes de continuar a ler, não quer tentar descobrir?

1ª INVESTIGAÇÃO

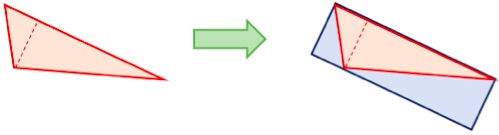
Comecemos por provar que o maior triângulo que se pode inscrever num retângulo vai ter metade da área do retângulo. Com efeito, nos vários casos possíveis, o triângulo vai ter a base igual a uma dimensão do retângulo e a altura igual à outra.

Dado então um triângulo qualquer, o menor retângulo que o poderá incluir vai ter, pelo menos, o dobro da área.

Será sempre possível com exatamente o dobro? A resposta é afirmativa. Basta construir o retângulo com base igual ao maior lado do triângulo e altura igual à altura do triângulo.

 
2ª INVESTIGAÇÃO

Dado um retângulo de medidas 1x4 unidades, qual será a área do menor triângulo capaz de o “tapar”?

Para rentabilizar ao máximo, os vértices do retângulo deverão coincidir com os vértices do triângulo e/ou ficar sobre os seus lados.

1º Caso – Triângulo retângulo com o vértice do ângulo reto a coincidir com um vértice do retângulo.

Temos de descobrir que medida deve ter o cateto AB para a área ser mínima. Analiticamente, é um pouco trabalhoso e não é muito fácil. Mas um programa de geometria dinâmica permite-nos fazer a construção, alterar o comprimento do cateto deslocando o ponto A, e observar como varia a área do triângulo.

 
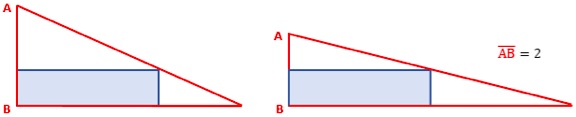
Rapidamente se descobre que a área é mínima quando o cateto AB mede duas unidades. A área do triângulo é igual a 8, o dobro da do retângulo.

2º Caso – Triângulo não retângulo com um lado sobre a base do retângulo.

Novamente com programa de geometria dinâmica, mantemos o ponto B fixo e construímos um triângulo de altura AB como se vê na figura. Deslocando A, fazemos variar a altura e procuramos a área mínima.

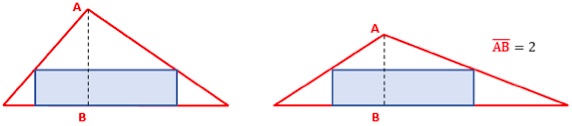
Também aqui isso acontece quando o cateto AB mede duas unidades e a área do triângulo é igual a 8, o dobro da do retângulo.

Fizemos o estudo para um retângulo 1x4 mas, prolongando a investigação, podemos generalizar.

Dado um retângulo 1xa, o menor triângulo que o cobre vai ter área igual a 2a.