100 Problemas por José Paulo Viana
Clube de Matemática SPM - Eixos de Opinião maio de 2017

100 Problemas por José Paulo Viana - Três pontos e um círculo
Clube de Matemática SPM - Eixos de Opinião maio de 2017
INVESTIGAÇÃO
Dados três pontos quaisquer do plano, quanto mede o diâmetro do menor círculo que contém esses pontos?
Leitor, antes de continuar a ler, não quer tentar descobrir?

Claro que o círculo vai depender da posição relativa dos pontos e das distâncias entre eles.
Seja M a maior das distâncias entre os pontos. Designemos por A e B os pontos que estão à distância M.
Tracemos as circunferências de raio M e centros em A e B. O terceiro ponto, C, tem de estar no interior das duas circunferências, visto que as distâncias de C, quer a A quer a B, são menores ou iguais a M.
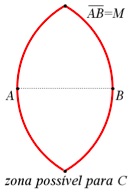
Com centro no ponto médio do segmento AB, desenhemos a circunferência que passa em A e em B.
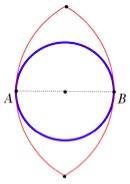
Não há círculo menor do que este, agora traçado, que inclua A e B. O seu diâmetro mede M.
Se o ponto C pertencer a este círculo, o problema está resolvido. Note-se que isto acontece se o triângulo ABC for obtusângulo ou retângulo (em C).
Se o triângulo ABC for acutângulo, o ponto C está fora do círculo traçado (mas dentro da zona permitida).
Nesse caso, o menor círculo que contém os pontos é o que fica definido pela circunferência que passa pelos três pontos.
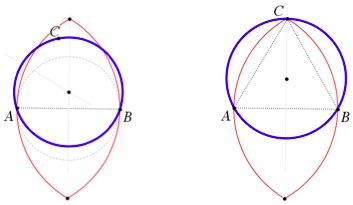
O pior dos casos acontece se o ponto C coincidir com um dos “vértices” da zona permitida, com o triângulo a ser equilátero. Nesta situação, o diâmetro do círculo é
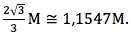
PROLONGAMENTO
E se, em vez de três, tivermos um conjunto finito de pontos?
Entre que valores, em função da maior das distâncias entre pontos, pode variar o diâmetro do menor círculo que os contém?
Não querem pensar um pouco nisto?

