Se e Só Se por José Carlos Pereira

Este artigo é a continuação do meu último texto. Como tal, caso ainda não o tenha feito, convido-o a ler aqui a primeira parte.

Depois de finalizado o estudo das funções trigonométricas, passa-se para o estudo das funções exponencial e logarítmica de base a, tanto no caso a > 1 como no caso 0 < a < 1.  Antes disso, abordam-se os juros simples e compostos e introduz-se o número de Neper. O que vem a seguir não tem diferenças significativas em relação ao programa anterior. Além de serem estudadas todas as características destas funções (domínios, contradomínios, zeros, intersecções dos gráficos com os eixos coordenadas, sinal, injectividade, monotonia, assimptotas, funções derivadas), são referidos os limites notáveis que envolvem funções exponenciais e logarítmicas. A saber: 

    

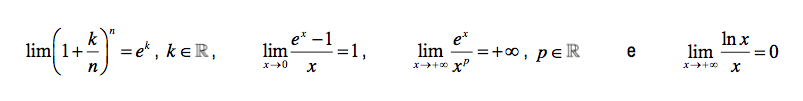
O programa refere especificamente estes limites como notáveis e não outros, pelo que, com um grau de certeza elevado, é de esperar que para resolver qualquer outro limite que envolva limites notáveis, se tenha de o reduzir a um destes. O leitor mais atento terá notado que entre estes quatro não está o limite notável:  

De facto este limite saiu do programa, razão pela qual não pode agora ser utilizado da forma como estávamos habituados. Mais uma vez, para resolver limites que o envolvam teremos de o reduzir a um dos limites notáveis que constam do programa. Neste caso o mais natural será reduzir a um do tipo:

Outra novidade do programa é partir de uma equação diferencial do tipo y’ = k y, k∈IR, para estudar os vários modelos exponenciais: decaimento radioactivo, lei de Newton do arrefecimento/aquecimento e crescimento populacional. Os modelos logarítmicos estão ausentes deste programa. 

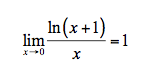
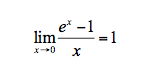
A novidade absoluta, pelo menos em relação aos programas mais recentes, é a introdução do tema Primitivas e Integrais, que, nestes dois primeiros anos de vigência do Novo Programa, será facultativo. Serão estudadas apenas as primitivas imediatas ou quase imediatas e as principais propriedades dos integrais que depois serão utilizadas para o cálculo de áreas limitadas por gráficos de funções.

O tema Números Complexos é o último a ser tratado. Em relação ao programa anterior a grande distinção é o desaparecimento da notação r cis(θ ) para representar um número complexo na forma trigonométrica que é substituída pela notação que recorre à exponencial complexa:

    

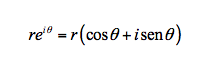
Esta é a principal diferença, mantendo-se tudo o resto praticamente igual. 

Uma nota final em relação ao Exame Nacional. Já não é a primeira vez que abordo este assunto no “Se e Só Se”, mas estamos cada vez mais próximos de Junho de 2018 e até agora pouco se sabe sobre a prova de exame que se irá realizar nesse mês. É urgente que o IAVE publique o documento com as informações relativas a essa prova (que pelo que se sabe conterá alguns exemplos de itens e critérios) e pelo menos prova modelo. Seria uma ajuda preciosa para os professores, mas mais importante, para os alunos.

Convido-o a deixar o seu comentário sobre este artigo na página do Facebook do Clube SPM.