100 Problemas por José Paulo Viana - O Velho Problema do Urso

Hoje vamos falar de um antigo problema, que tem soluções curiosas e prolongamentos interessantes.

Comecemos pelo seu enunciado original.

Um caçador partiu de um certo local. 

Caminhou um quilómetro para sul, depois um para oeste e a seguir um para norte, voltando ao ponto de partida.

De que cor era o urso? 

Nos últimos tempos, o enunciado foi alterado, adaptando-o ao “politicamente correto”. Em vez de um caçador, o personagem principal passa a ser um fotógrafo que dispara para captar a imagem do urso. 

 

Quando se depara pela primeira vez com este problema, surge uma certa perplexidade. O que é que as andanças do caçador têm a ver com a cor do urso?

Leitor, se nunca resolveu o problema, talvez valha a pena tentá-lo antes de continuar a ler.

Antes de avançar, recapitulemos algumas coisas sobre a Terra e sobre os pontos cardeais.

A Terra não é uma esfera perfeita, mas quase…

Existem montanhas e depressões mas, se as compararmos, são inferiores às rugosidades da casca de uma laranja. Com efeito, o Everest teria uma altura inferior a 0,09 milímetros se a Terra fosse do tamanho desse citrino.

Também existe um achatamento nos polos. O raio equatorial da Terra é de 6378 quilómetros e o raio polar de 6357. Numa laranja grande, isso equivaleria a um achatamento de 0,1 mm em cada polo.

Imaginemos agora que vamos fazer os movimentos do caçador: um quilómetro para sul, depois um para oeste e a seguir um para norte. A nossa experiência diz-nos que será qualquer coisa como isto.

De modo nenhum voltaríamos ao ponto de partida.

Para ultrapassar esta dificuldade, temos de recapitular o que é caminhar na direção dos pontos cardeais.

Andar para norte ou para sul é seguir ao longo de um meridiano. Os meridianos são círculos máximos que passam nos polos. Os círculos máximos têm centro no centro da Terra e correspondem ao caminho mais curto entre dois pontos. A cada meridiano está associada uma longitude.

Andar para oeste ou para leste é seguir ao longo de um paralelo. Os paralelos já não são círculos máximos, com exceção do equador. São circunferências equidistantes dos polos, cujo centro é um ponto do eixo da Terra e caminhar sobre um paralelo não é seguir pelo caminho mais curto. A cada paralelo está associada uma latitude.

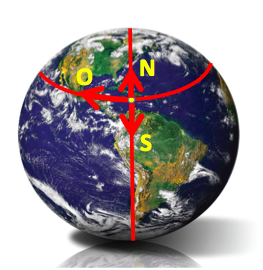
Como os paralelos são circunferências equidistantes dos polos, isto dá-nos a pista para a solução. O nosso caçador (ou fotógrafo…) está no Polo Norte. Partindo daí, qualquer que seja a direção em que avance, está sempre a caminhar para sul. Percorrido um quilómetro, vira para oeste e segue mais um quilómetro ao longo de um paralelo. Depois, mais um quilómetro para norte, em direção ao Polo, terminando no sítio de onde partiu.

Como só há um tipo de urso no Ártico, a resposta é: o urso era branco.

Esquecendo o urso, podemos ir mais longe. 

Poderíamos pensar no Polo Sul, mas não serve, porque dali só se pode ir para norte, qualquer que seja a direção. Mas estamos perto…

Com efeito, imaginemos uma circunferência equidistante do Polo Sul (um paralelo) de perímetro um quilómetro (a vermelho na figura) e uma outra (a azul), equidistante um quilómetro da primeira.

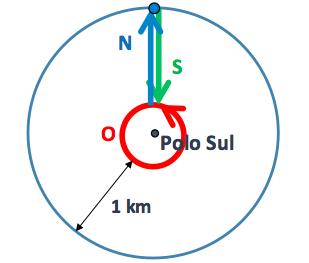
Se partirmos de um ponto qualquer da circunferência azul e andarmos um quilómetro para sul (ou seja, em direção ao polo), chegamos à circunferência vermelha. Andar para oeste é avançar sobre ela, e um quilómetro depois demos uma volta completa. Mais um quilómetro para norte e voltamos ao ponto de partida.

Mas ainda há mais soluções. Se a circunferência vermelha tiver meio quilómetro de perímetro, daremos duas voltas sobre ela para percorrer um quilómetro. Logo, se partirmos de uma circunferência azul a um quilómetro, temos outra infinidade de soluções.

E mais, seguindo o mesmo raciocínio, com a circunferência vermelha a ter um terço de quilómetro, ou um quarto, ou…

Resumindo, esta nova versão, já sem urso porque na Antártica não existem estes animais, tem uma infinidade (numerável) de infinidades (contínuas) de soluções.

No próximo mês veremos mais um prolongamento deste problema.