(U)Ma Temática Elementar por José C. Santos
Clube de Matemática SPM - Eixos de Opinião julho de 2016
|
|
José Carlos Santos - Departamento de Matemática da FCUP Dia 21 de cada mês
|
(U)Ma Temática Elementar por José Carlos Santos - Ramanujan
Clube de Matemática SPM - Eixos de Opinião julho de 2016
Clube de Matemática SPM
Facebook Clube SPMEstreou este mês o filme O homem que viu o infinito, que descreve a vida adulta do matemático indiano Srinivasa Ramanujan. Gostaria de falar aqui sobre algumas contribuições dele para a Matemática que possam ser vistas, pelo menos em parte, como fazendo parte da Matemática Elementar.

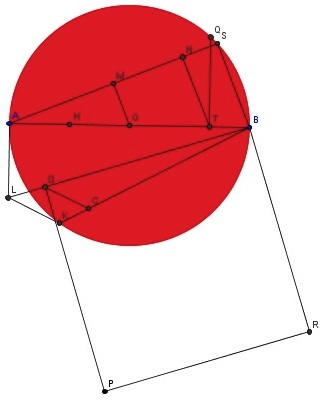
Uma delas tem a ver com a quadratura do círculo e já foi referida nesta rubrica. Fazer a quadratura do círculo consiste em construir, usando unicamente régua e compasso, um quadrado com a mesma área que a de um círculo dado e já se sabe, desde 1882, que este problema não tem solução. Isso não impede que haja construções que estejam muito próximas de estar correctas e Ramanujan fez uma tal construção. Na figura abaixo pode-se ver um círculo de centro O e diâmetro AB. Ramanujan explicou em 1913 como obter um quadrado que teria a mesma área que o círculo caso π fosse igual a 355/113 (já agora, π é aproximadamente 3,1415926 e 355/133 é aproximadamente 3,1415929). O método é este:
1. Seja H o ponto médio de AO.
2. Seja T o ponto do segmento OB tal que o comprimento de TB seja um terço do de OB.
3. Seja Q um ponto da circunferência de modo que o segmento TQ seja perpendicular a AB.
4. Seja S um ponto da circunferência tal que o comprimento do segmento BS seja igual ao do segmento TQ.
5. Sejam M e N pontos do segmento AS tais que os segmentos OM e TN sejam paralelos ao segmento BS.
6. Seja K um ponto da circunferência tal que A seja equidistante de K e de M.
7. Seja L um ponto tal que o segmento AL seja tangente à circunferência e tenha comprimento igual ao de NM.
8. Seja C um ponto do segmento BK tal que B seja equidistante de C e de H.
9. Seja D o ponto do segmento BL tal que os segmentos CD e LK sejam paralelos.
10. Sejam P e R tais que os pontos B, D, P e R formem os vértices de um quadrado dos quais um dos lados seja o segmento BD.
E até que ponto é que a área do quadrado está próxima da do círculo? Bastante próxima: a área do quadrado só excede a do círculo em menos de uma milionésima parte. O facto de π estar bastante próximo de 355/113 não é uma descoberta de Ramanujan. Mas Ramanujan não se limitou a esta aproximação e descobriu «por métodos empíricos» (palavras dele) que uma aproximação ainda melhor de π é a raiz quarta 92 + 192/22… e também fez uma quadratura aproximada do círculo baseada neste facto.
Mas o resultado mais famoso de Ramanujan relativamente a π é a seguinte fórmula extraordinária:
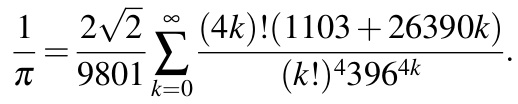
E o que é que tem de extraordinário? Já vimos nesta rubrica como obter π como uma soma infinita. O que há de particular nesta fórmula é a rapidez com que nos dá π com precisão. Se virmos quanto dá esta expressão se usarmos somente a primeira parcela da soma, obtemos logo π com um erro aproximadamente igual a 10-8, se usarmos as duas primeiras parcelas, o erro é aproximadamente igual a 10-16 e assim por diante.
Quem achar que isto já não é matemática elementar, tem alguma razão. Voltemos então a essa Matemática. Ramanujan interessou-se por quadrados mágicos, ou seja, por quadrados de números naturais nos quais a soma de qualquer linha, de qualquer coluna e de qualquer diagonal dá sempre o mesmo valor. Por exemplo, o seguinte quadrado (mencionado por Ramanujan) é um quadrado mágico:
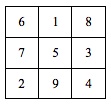
Construir quadrados mágicos tem toda uma teoria por trás. Por exemplo, Ramanujan provou que, num quadrado mágico com 3 linhas e 3 colunas, os números da linha do meio, da coluna do meio e das duas diagonais estão sempre em progressão aritmética. Além disso, Ramanujan criou quadrados mágicos bem maiores do que este, incluindo um quadrado com 8 linhas e 8 colunas. Mas o seu quadrado mágico mais famoso é mais pequeno. É este:
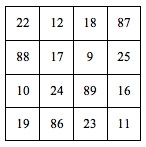
E o que é que tem de especial este quadrado mágico? A primeira linha. É que Ramanujan nasceu a 22 de Dezembro de 1887!


