100 Problemas por José Paulo Viana - Um Passeio de Bicicleta
Eixos de Opinião de maio de 2018

Título: Um Passeio de Bicicleta
Há problemas que nos podem surpreender pelos mais variados motivos. Um deles é o seguinte.
A Isabel foi de bicicleta visitar a Beatriz, que mora longe. Quer para lá, quer no regresso, a velocidade foi de 12 km/h nas subidas, de 20km/h nas zonas planas e de 60 km/h nas descidas. O tempo total da viagem de ida e volta foi de exatamente duas horas.
Qual é a distância entre as casas das duas amigas?
Quando começamos a pensar em como chegar à resposta surge-nos logo uma dificuldade: não temos nenhuma informação sobre que proporções do percurso são a subir, a descer e na horizontal. Será possível descobrir o que se procura sem saber mais nada?

Apesar destas reticências, avancemos na resolução.
Representemos por S as distâncias que, à ida, são a subir, por D as que descem e por H as horizontais. Como os tempos são iguais às distâncias a dividir pelas velocidades, temos:
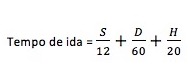
No regresso, os percursos a subir passam a ser a descer e vice-versa. Então:
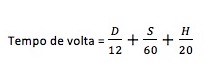
Como o tempo total foi de duas horas, vem:
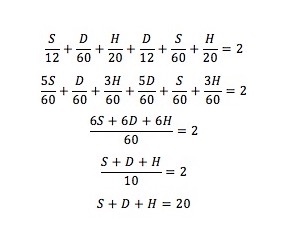
Surpreendentemente, chegámos à resposta: a Beatriz mora a 20 quilómetros de casa da Isabel. Não sabemos é que partes do percurso são a subir, a descer ou na horizontal.
O facto de, com tão pouca informação, termos resolvido o problema leva-nos a ter de investigar porque é que isto aconteceu. É que, se as velocidades fossem, por exemplo, de 12, de 15 e de 60 km/h, o problema seria irresolúvel, como os leitores poderão confirmar. O resultado iria depender da proporção de subidas e descidas no percurso.
Vejamos então o que se passou no nosso caso.
Como as subidas à ida são descidas à volta, e vice-versa, na viagem completa o total de subidas é igual ao total de descidas. Representemos por Y o total de subidas (igual ao total de descidas) e calculemos a o tempo gasto nos percursos não planos.
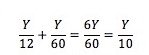
Então, a velocidade média nos percursos não planos (igual à distância 2Y a dividir pelo tempo) é:
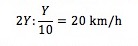
Ora esta velocidade é precisamente igual à velocidade nas zonas planas. Ou seja, não interessa se há muitas ou poucas subidas, a velocidade média vai ser sempre de 20 km/h.
Do ponto de vista matemático, estamos perante a média harmónica dos números 12 e 60, que é 20.
Recordemos: a média harmónica m.h. de dois números a e b é “o inverso da média dos inversos” desses números.
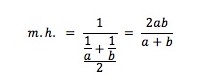
Por curiosidade, podemos procurar pares de números inteiros cuja média harmónica também seja inteira. Os primeiros que aparecem constam desta tabela
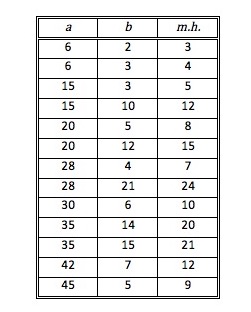
A partir destes, que são os elementares, podemos obter outros, multiplicando os três elementos de uma linha por uma constante. Os dados do nosso problema correspondem à linha (30, 6, 10) multiplicada por 2.

