100 Problemas por José Paulo Viana

No mês passado, fizemos uma primeira abordagem a este problema:

Imaginemos que existem N ditadores na Terra. Como colocá-los o mais afastado possível uns dos outros? Ou seja, como fazer para que a menor das distâncias entre quaisquer dois deles seja máxima? Qual é essa distância?

Até ao momento, são conhecidas soluções para N de 2 a 12, 14 e 24. Usando algoritmos de aproximações sucessivas, encontraram-se também soluções para os valores de N até 60 (além de outros casos isolados) mas que têm de ser consideradas aproximadas visto não se ter conseguido demonstrar que são verdadeiras soluções.

Hoje vamos ver que o problema até muda de nome, que existem algumas curiosidades associadas e que tem várias aplicações.

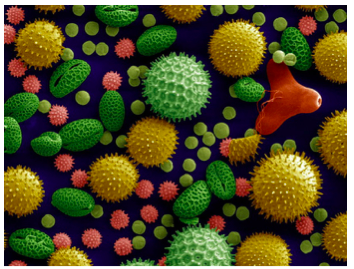
Os grãos de pólen de algumas plantas são esféricos, com várias aberturas ou com excrescências à sua superfície.

Em 1930, o botânico holandês R. M. L. Tammes, ao estudar estes grãos, reparou que as aberturas se distribuíam de modo a maximizar a menor das distâncias entre elas. 

 

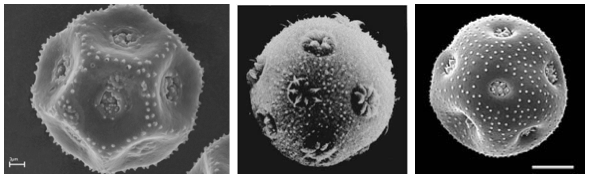
Ou seja, a natureza encontrou, através dos grãos de pólen, soluções para o problema dos ditadores.

Devido a isto, o problema ganhou novo nome e começou a ser conhecido também por “Problema de Tammes”.

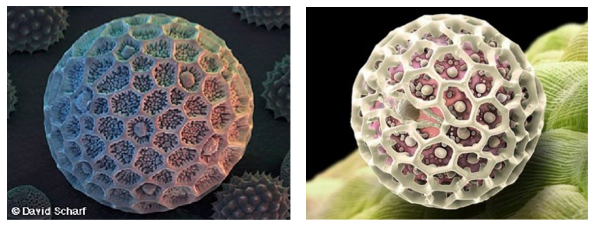
As soluções (exatas ou aproximadas) têm sido usadas em várias situações. Vejamos algumas.

A bola de golf, por questões de aerodinâmica, tem cerca de 500 reentrâncias que devem estar o mais uniformemente dispostas.

A distribuição de combustível por reatores nucleares esféricos deve ser tal que maximize o mínimo das distâncias entre pares de entradas de combustível.

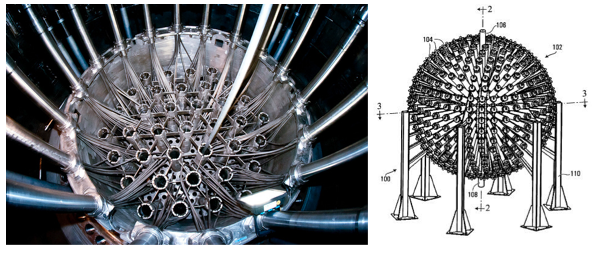
O mesmo se passa com a distribuição de eletrões em redor do núcleo atómico para que seja mínima a energia potencial eletrostática.

Finalmente, uma versão mais complicada do problema Tammes teve de ser resolvida para se decidir onde colocar os satélites dos sistemas de localização (Galileo, GPS, GLONASS). Teoricamente, é preciso que haja, em cada momento, quatro satélites visíveis (acima da linha do horizonte). Na prática, como pode haver falhas na captação dos sinais, haverá sempre um mínimo de seis satélites à vista (e um máximo de doze). Para isso, foram lançados 24 satélites, em 6 órbitas distintas de 4 satélites cada. 

 

Na internet podemos ver animações que mostram o funcionamento destes sistemas.
https://en.wikipedia.org/wiki/File:ConstellationGPS.gif
http://www.linksolutions.com.br/tecnolink-como-funciona-o-gps/