(U)Ma Temática Elementar por José C. Santos
Clube de Matemática SPM - Eixos de Opinião abril de 2017
|
|
José Carlos Santos - Departamento de Matemática da FCUP Dia 21 de cada mês
|
(U)Ma Temática Elementar por José Carlos Santos - Linhas rectas em superfícies curvas
Clube de Matemática SPM - Eixos de Opinião abril de 2017
Clube de Matemática SPM
Facebook Clube SPMTítulo: Linhas rectas em superfícies curvas
Imagine uma circunferência e um ponto no espaço, estando o ponto fora do plano que contém a circunferência. O que é que se obtém se se unir, por um segmento de recta o ponto dado a cada um dos pontos da circunferência? A resposta é simples: um cone (que em geral, não será um cone recto), como na figura abaixo.

Imagine agora novamente uma circunferência no espaço, bem como uma recta (que não esteja contida no plano que contém a circunferância). Se se traçaram todas as rectas que passam pela circunferência dada e que são paralelas à recta dada, o que é que se obtém? Desta vez obtém-se um cilindro (mais uma vez, não necessariamente recto).

Até aqui, nada de especial. Quem olhar para um cone ou para um cilindro, vé logo lá uma data de rectas (ou de segmentos de recta). Mas há outras superfícies formadas por rectas que não parecem ter essa propriedade. Vejamos um exemplo: o hiperbolóide de uma folha:
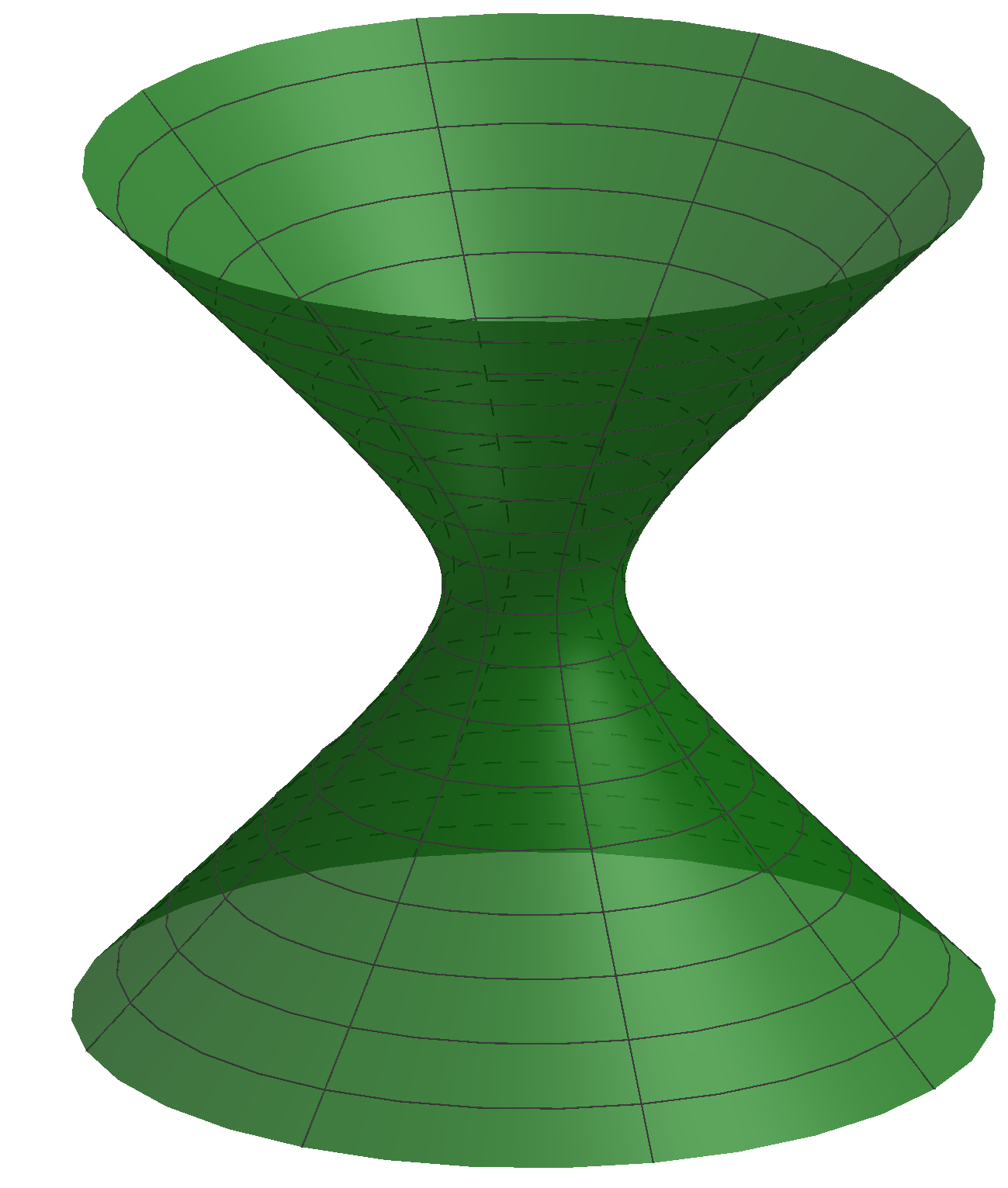
Não está a ver ali nenhuma recta? É natural, mas elas estão lá. De facto, por cada ponto daquela superfície passam duas rectas que estão inteiramente lá contidas (ao contrário do cilindro ou do cone). A seguinte figura (formada unicamente por rectas) torna clara a existência de rectas no hiperbolóide de uma folha:
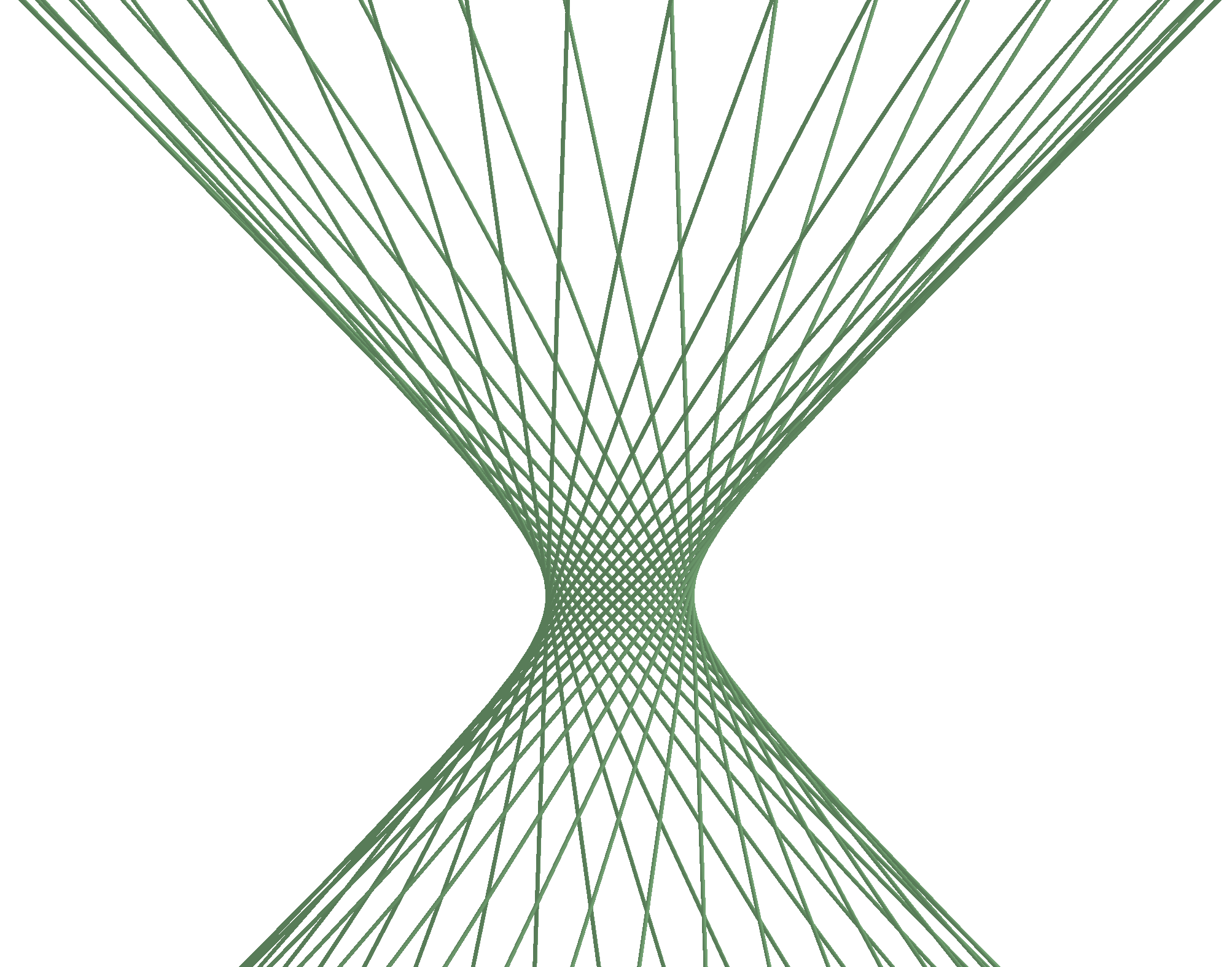
Uma ilustração particularmente bem conseguida desta propriedade pode ser vista aqui.
Outra superfície com esta propriedade é o parabolóide hiperbólico:
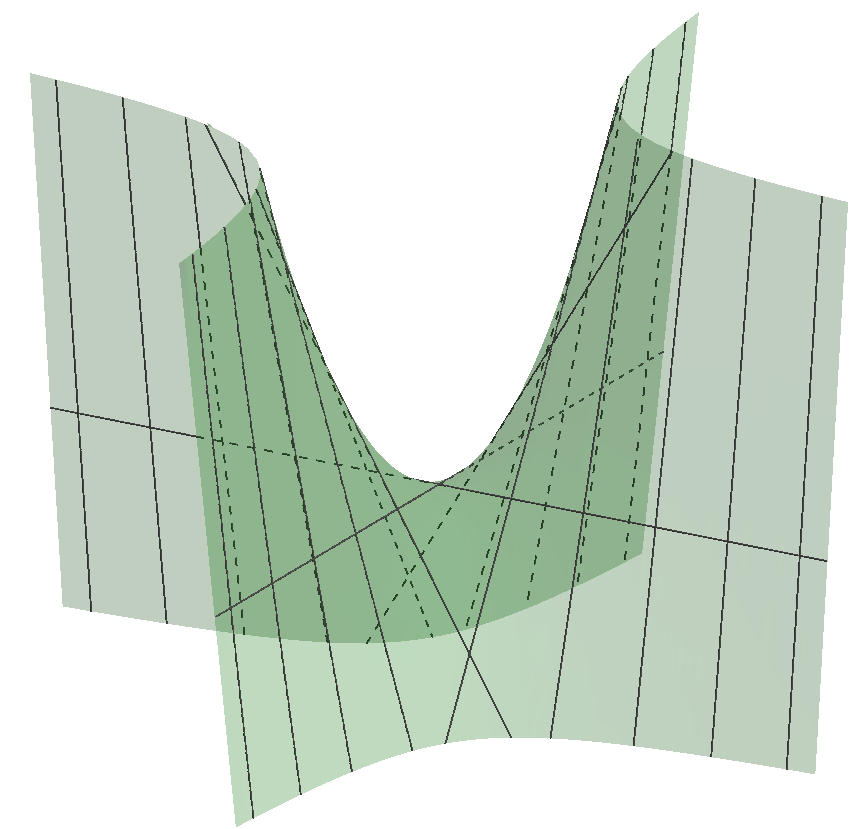
Neste caso, é difícil duvidar da existência das rectas, visto que estão na figura!
Quando uma superfície tem a propriedade de ser formada por rectas, então é relativamente fácil construí-la e usá-la em Arquitectura e em Engenharia. Por exemplo, as torres de arrefecimento das centrais de energia são geralmente hiperbolóides de uma folha. Por outro lado, há vários exemplos de edifícios cujas coberturas são parabolóides hiperbólicos.




