Diagonais por Rui Gonçalves
Matemática - Clube de SPM - Dezembro de 2017
|
|
“Diagonais é uma rubrica onde se falará da aprendizagem da matemática. Serão alvo de análise os dois últimos anos do ensino secundário e as cadeiras da área científica de matemática nos dois primeiros anos dos cursos de Engenharia. Abordaremos também temas relacionados, como os programas e a metodologia seguida na aprendizagem da matemática nos cursos superiores de Engenharia.”
Rui Gonçalves - Professor de Matemática da FEUP. Membro Integrado do Laboratório de Inteligência Artificial e de Apoio à Decisão - LIAAD INESC TEC |
Diagonais por Rui Gonçalves - Análise 1 sem complexos?
Matemática - Clube de SPM - Dezembro de 2017
Clube de Matemática SPM
Facebook Clube SPMTítulo: Análise 1 sem complexos?
No mês passado falamos na introdução dos números complexos no 12º ano que de alguma forma se teriam que se justificar com aplicações para não ser apenas uma ferramenta sem qualquer utilidade à vista.
Este mês iremos falar da utilização de complexos (Identidade de Euler) na primeira disciplina de análise matemática no 1º ano da faculdade dos cursos de Matemática, Engenharia, Economia e afins.
Os leitores que frequentaram o ensino superior tiveram contacto com a integração. Terão com certeza passado algumas horas a integrar e a aplicar técnicas de integração, a substituição de variável e a integração por partes.
Certamente se recordam da integração de funções envolvendo o seno e cosseno. Estas funções são persistentes obrigando muitas vezes a recorrer à integração por partes.
Mas estas funções exprimem-se simplesmente sob a forma de exponenciais usando a identidade de Euler. Temos,
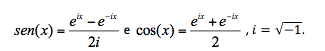
Por exemplo, para obter o integral ∫ex cos(x) dx usando a habitual abordagem teríamos que recorrer ao uso consecutivo da integração por partes. Porém, usando análise complexa, o integral é simplesmente,
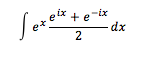
E assim,
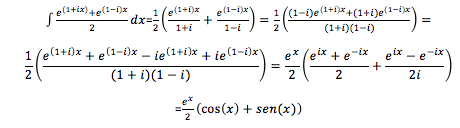
Ao pensarmos em integrar potências de seno e cosseno com expoente como ∫sin (x)4 dx antecipamos uma grande dor de cabeça, como é que nos safamos desta?
Mas usando a fórmula de Euler,
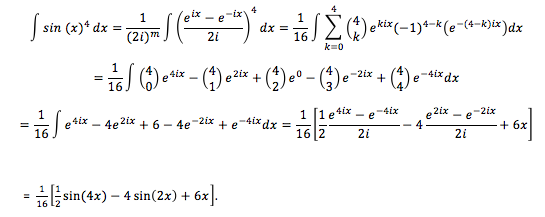
Convidamos o leitor a implementar a fórmula para o ∫ sin (x)m dx. Terá que usar o binómio de Newton e separar o caso em que m é par do caso em que m é impar.
O uso da fórmula de Euler é usado com sucesso nos tipos de integrais que vimos e também em integrais do tipo sin(x)m cos(x)n. Os interessados em mais informação podem consultar o recente artigo Teaching Mathematics and Its Applications, (2016), 35, 236-244.
Fiquem bem tenham boas festas e até Janeiro.


