Contos de 3º Grau - Hollywood (13º Episódio/4ª Parte)
Por José Veiga de Faria
Contos de 3º Grau por José Veiga de Faria - Hollywood (13ª episódio/4ª Parte)
Clube SPM
Clube de Matemática SPM
Facebook Clube SPM 


Título: Hollywood...
1ª Parte por Carlos Marinho - Dia 1
![]()
Peter Michael Kerkman acaba de chegar a casa. Uma mansão de alguns milhões de dólares recebe-o entre alarmes, segurança, silêncios e uma falta de privacidade que o incomodava muito. Entrou pela porta principal, com a estatueta dourada ganha minutos antes na cerimónia dos Óscares. Não percebia como em poucos meses se tornara uma figura conhecida mundialmente. Afinal, só tinha feito um filme. De repente, aos 21 anos viu a sua conta bancária engordar de uma forma indómita, aumentando os problemas, não financeiros, mas de preocupação do seu modus vivendi.
Sentia-se só. Precisava de algo muito forte para o acalmar. Foi ao escritório, abriu o cofre e tirou de lá um saco. De dentro tirou um saco de gomas e um caderno que dizia na capa “0 Problema do Caixeiro Viajante”.
Peter descendia do matemático inglês Thomas Penyngton Kerkman, um dos primeiros a estudar este problema sem solução.
Peter tinha interrompido a licenciatura em matemática por causa da fama onde era um aluno brilhante.
Abriu o bloco e sorriu...
2ª Parte por José Carlos Santos - Dia 6
![]()
Grande parte do caderno era formado por textos manuscritos de Thomas Kerkman relativos ao Problema do Caixeiro Viajante. Alguns tinham sido publicados, mas a maior parte, que continham ideias inconclusivas sobre como resolver o problema, permaneciam inéditos. O caderno tinha permanecido na posse da família e vários descendentes de Thomas Kerkman tinham acrescentado observações. O próprio Peter Michael fizera isso.
O cansaço apoderou-se rapidamente dele. Isso deixou-o irritado, pois gostava de planear cada dia na véspera e estava com dificuldade em concentrar-se. Tinha que ir a Nova Iorque, onde estava a trabalhar num filme, mas também tinha que marcar uma reunião com o seu agente e um produtor importante de Dallas, para além de ter outras tarefas. Começou a pensar em qual seria a maneira mais eficiente de fazer isso tudo, ou seja, a que o faria viajar menos.
E, bruscamente, todo o cansaço desapareceu. Peter Michael ficou imóvel, com os olhos arregalados e o coração muito agitado. Parecia-lhe que tinha obtido maneira de resolver não só o seu problema como todos os problemas do mesmo género!
3ª Parte por Filipe Oliveira- Dia 11
![]()
Rabiscou, ofegante, uma dúzia de páginas. Aplicou o seu método a um bom número de exemplos simples, em que a resolução pode ser facilmente obtida por métodosad-hoc, e tudo parecia bater certo. Considerou então um exemplo em que todas as cidades a visitar pelo caixeiro viajante se encontravam alinhadas, todas com exceção de uma. Infelizmente, nesta situação, era bastante claro que o seu método falhava...preconizava uma ziguezaguear entre as diferentes localizações que era tudo menos optimal.
Largou as gomas e serviu- se de um whisky. Um Dalmore Single Hiland Malt Scotch, de 62 anos, cujo preço da garrafa ronda tradicionalmente os 55.000 dólares. É evidente que um rapaz de 21 anos não tem experiência suficiente para apreciar esta fineza da distilação e os leves e subtis aromas herdados do malte e do casco da pipa, mas Peter, com esta aventura no mundo do cinema, estava a ficar com a mania das grandezas. Levou o copo à boca e fez uma careta, como que desagradado.
Pensou na sua última conquista, Rosemary Lindon - uma ruiva sulfurosa do bairro de Hollywood Hills – e estabeleceu um paralelo com o problema do caixeiro viajante. Tudo parecia perfeito até um dado momento...
4ª Parte por José Veiga de Faria - Dia 16
![]()
Peter estava excitado e muitíssimo assustado. Começava a sentir-se embriagado: com o scotch mas também com aquela explosiva sensação de estar perto resolver um problema que lhe traria uma fama imortal e em breve lançaria o mundo num caos. Nada é perfeito mas há limites para a imperfeição admissível. Voltou a encher o copo com o Highland Scotch e entornou-o de um trago.
Bolas! Ele sabia que o problema que tinha em mãos era um daqueles problemas, ditos de classe NP-Hard, que se admitissem um algoritmo que desse uma solução em tempo que crescesse lentamente (de forma polinomial) com o número de cidades, então qualquer outro problema de uma vasta classe de problemas importantes admitiria um algoritmo capaz de dar uma solução com idêntica rapidez: alguém acabaria por encontrá-lo.
Em particular o problema da factorização dum inteiro em primos em que se baseava toda a segurança da Net. O mundo ficaria à beira do caos e ele nos píncaros da fama. Engoliu outro copo de scotch: as tonturas aumentavam. Embrenhou-se no código como um louco.
Cinco horas depois sentiu que tinha eliminado todos os erros! A garrafa estava no fim…
Fez um teste simples enquanto, com a cabeça meia pendente sobre o teclado, repetia com voz cada vez mais arrastada: todas alinhadas com exceção de uma.
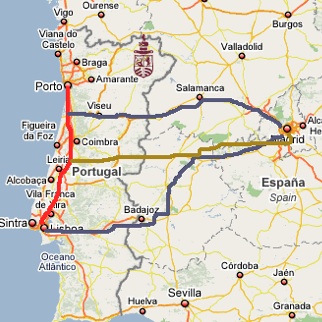
Digitou: Porto, Lisboa, Faro, Madrid. Com o coração a bater consultou o layout do computador: Porto -> Faro -> Madrid -> Lisboa -> Porto.
5ª Parte Sílvio Gama - Dia 21
![]()
6ª Parte por Paulo Correia - Dia 26
![]()


