Teoria de Jogos por Alda Carvalho - Almejo do Jogador
Eixos de Opinião de Março de 2020

Alda Carvalho - Docente do Ensino Superior e Investigadora do CEMAPRE/ISEG
Título: Almejo do Jogador
Neste artigo falaremos de jogos com componente aleatória como, por exemplo, o GAMÃO. Neste tipo de jogos, uma vez que existe componente aleatória, é comum jogar-se mais do que uma partida para atenuar o factor sorte.
Imagine que Pierre vai jogar um match com Blaise até alguém conseguir ganhar 5 partidas. Pierre joga melhor do que Blaise, ele ganha-lhe 60% das vezes. Assumindo que existe independência entre as partidas, qual é a probabilidade de Pierre ganhar o match?
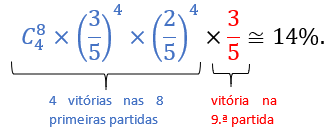
Uma vez que o match será ganho por quem conseguir atingir 5 vitórias, o match terá entre 5 e 9 partidas. Comecemos então por uma questão mais simples: qual é a probabilidade de Pierre ganhar o match na 9.ª partida?
Para que isso aconteça, Pierre terá de conseguir 4 vitórias nas primeiras 8 partidas e vencer a 9.ª partida, isto é,
Em geral, sendo p a probabilidade de sucesso numa experiência aleatória, a probabilidade de haver k sucessos em exactamente n repetições da experiência é dada por
P(X = n) = Ck-1n-1×(1-p)n-k×pk
Trata-se da função massa de probabilidade da distribuição Binomial Negativa. Também se pode utilizar a função massa de probabilidade da Binomial, considerando X~BinomialNegativa(k,p) e X'~Binomial(n-1,p), tem-se
P(X = n) = P(X´=k-1)×p.
Voltemos à questão: qual é a probabilidade de Pierre ganhar o match?
Nesse caso, não se trata apenas da probabilidade de Pierre ganhar o match apenas na 9.ª partida, mas também na 8.ª, 7.ª, 6.ª e 5.ª (número mínimo de partidas necessárias para ganhar o match), ou seja,
P(X=9)+P(X=8)+⋯+P(X=5) = P(X≤9).
Trata-se de uma probabilidade cumulativa, ou seja, a função distribuição da Binomial Negativa.
Comecemos por dividir em dois casos, ou Pierre ganha o match nas 8 primeiras partidas ou Pierre ganha o match na 9.ª partida.
Neste caso, X~BinomialNegativa(5,0.6) e X'~Binomial(8,0.6), tem-se
P(X≤9)=(1-P(X≤4))+P(X=4)×0.6≅73%.

Em geral, sendo X~BinomialNegativa(k,p) e X'~Binomial(n-1 ;p), tem-se
P(X ≤ n)=P(X´≥ k) + P(X´= k-1)×p.
Ao contrário da distribuição Binomial, a distribuição Binomial Negativa não está disponível na maioria das calculadoras. Para cálculos envolvendo probabilidades cumulativas, esta ligação entre os dois modelos facilita os cálculos.

