Teoria de Jogos por Alda Carvalho - Os Números e os Jogos
Eixos de Opinião de Maio de 2020

Alda Carvalho - Docente do Ensino Superior e Investigadora do CEMAPRE/ISEG
Título: Os Números e os Jogos

Deixou-nos no mês passado o último dos três fundadores da Teoria de Jogos Combinatórios, John Conway (1937-2020). Entre importantes contribuições em Teoria de Números, Teoria dos Grupos Finitos ou Teoria de Códigos, destaca-se o seu contributo na Matemática Recreativa e na Teoria de Jogos Combinatórios. Juntamente com Richard Guy e Elwyn Berlekamp, foi co-autor da principal referência desta área, Winning Ways for Your Mathematical Plays (1982).
Em 1970, John Conway introduziu os números surreais. Quatro anos mais tarde, Donal Knuth publicou o livro Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness, uma obra de ficção onde esta fantástica ideia é apresentada. Mais tarde, no seu livro de 1976, On Numbers and Games, Conway desenvolveu a teoria dos números surreais e usou-os para analisar jogos combinatórios. Nas suas palavras, «...You get surreal numbers by playing games. I used to feel guilty in Cambridge that I spent all day playing games, while I was supposed to be doing mathematics. Then, when I discovered surreal numbers, I realized that playing games IS mathematics».
Um jogo combinatório satisfaz as seguintes condições:
1) Dois jogadores jogam alternadamente, geralmente denominados Louise (Left, bLue) e Richard (Right, Red);
2) Não há dispositivos de sorte como dados, cartas ou peões; em todos os momentos, cada jogador é conhecedor de toda a informação relativa a uma posição de jogo;
3) As regras de um jogo combinatório asseguram que, mesmo ignorando a regra da alternância, não há sequências infinitas de jogadas legais; o jogo está condenado a acabar;
4) Há uma condição de vitória que se executa após o último movimento efectuado (geralmente é usada a versão normal que estipula que o último a jogar ganha).
Um exemplo clássico desses jogos é o ARBUSTO AZUL E VERMELHO (BLUE-RED-HACKENBUSH). Neste jogo, Louise só pode retirar arestas azuis e Richard só pode retirar arestas vermelhas. À vez, cada jogador retira uma aresta. Todas as arestas que fiquem desligadas do chão saem automaticamente. O último a jogar ganha.
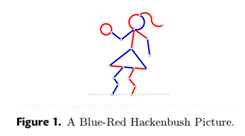
Nesta imagem, que está na primeira página do Winning Ways, se Richard retirar o cabelo, mais nenhuma aresta sai. No entanto, se Richard retirar o tronco, saem todas as arestas que perdem a ligação ao chão (braços, cabeça, cabelo). Quem terá vantagem, Louise ou Richard? A análise deste tipo de jogos fez com que uma nova teoria matemática ganhasse forma.
É usual representar os jogos combinatórios da seguinte forma:
{Opções da Louise |Opções do Richard}.
Trata-se de uma descrição recursiva, na medida em que as opções são também jogos.
Consideremos a posição seguinte:

Nesta posição, nenhum dos jogadores tem opções. Usando a notação de teoria de jogos combinatórios, por definição, estabelece-se que o valor do jogo { | } é 0.
Consideremos agora a posição seguinte:
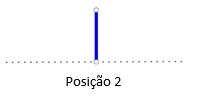
Neste caso, Louise tem uma jogada (tirar a aresta azul, indo para a posição anterior – 0) e Richard não tem opções. Louise ganha, independentemente de quem jogue primeiro. A forma do jogo é {0 | } e corresponde a uma vantagem de uma jogada para Louise. Por definição, {0 | } = 1. Naturalmente, uma aresta vermelha é { | 0 } = -1, o simétrico da posição 2. Neste caso, a vitória é do Richard, independentemente de quem for a jogar.
Uma posição mais interessante é a seguinte:
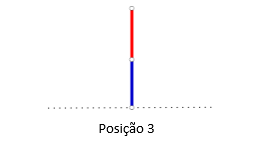
Neste caso, se for a Louise a jogar, remove a aresta azul e vai para a posição 1; se for o Richard a jogar, remove a aresta vermelha e vai para a posição 2, ou seja, a forma é {0 | 1}. Também nesta posição, Louise ganha independentemente de quem for a jogar. Uma primeira questão importante é a de saber qual das duas é melhor para Louise (posição 2 ou 3). Conway respondeu a esta questão usando a ideia simples que consiste em jogar a posição 3 lado a lado com o simétrico da posição 2 (aresta vermelha ligada ao chão). Como analogia, suponha que tem dois números: 2 e 1. O facto de 1 ser menor do que 2 faz com que 1-2<0. Aplicando a ideia a jogos, se a posição 3 for menor do que a posição 2 deverá fazer com que, jogando «posição 3 – posição 2», Richard ganhe sempre (jogando em primeiro ou em segundo lugar). De alguma forma, a ideia chave consiste em perceber que a adição dos números «corresponde» de alguma forma ao «jogar lado a lado». A frase «I discovered surreal numbers, I realized that playing games IS mathematics» significa exactamente isto: formalizando a soma disjunctiva («jogar lado a lado»), a estrutura obtida está magicamente ligada com a estrutura dos números reais. E isso é absolutamente surpreendente. Podemos, literalmente, jogar com os números reais.

Analisando esta posição, facilmente se percebe que Richard ganha, independentemente de quem começa. Uma segunda questão importante é a de saber quanto melhor é a posição 2. Aqui surge a quantificação e, com isso, a matemática.
São precisas duas cópias da posição 3 para se ter um equilíbrio com o simétrico da posição 2.

Ao analisar a posição 5, é possível verificar que quem joga perde. O que faz com que sejam necessárias 2 componentes iguais à posição 3 para equilibrar o simétrico da posição 2. Resumindo, a posição 3 é uma de duas partes iguais de um todo que é a posição 2. Por outras palavras, como o valor da posição 2 é 1, temos em mãos uma posição 3 cujo valor é ½ (uma espécie de meia jogada). Deve definir-se {0 | 1} = ½, para que a álgebra faça sentido. A descoberta de ½ em contexto de jogo foi um dos momentos de grande felicidade para Conway.

