Se e Só Se por José Carlos Pereira
Clube de Matemática SPM - Eixos de Opinião outubro de 2016
|
|
Nesta coluna pretendo partilhar todos os meses a minha opinião sobre questões relacionadas com a Matemática e com o seu ensino. Os leitores são convidados a comentar, com argumentos a favor ou contra, aliás é esse o objectivo desta coluna: discutir diferentes pontos de vista sobre o tema do artigo (dia 3 de cada mês).
José Carlos da Silva Pereira – Professor de Matemática, autor de livros escolares e responsável pelo site Recursos para Matemática. Ler artigos anteriores aqui. |
Clube de Matemática SPM - Eixos de Opinião outubro de 2016
Clube de Matemática SPM
Facebook Clube SPM
Título: Relembrar as Bases
No início deste ano lectivo, o novo Programa de Matemática A do Ensino Secundário entrou em vigor no 11.º Ano. O programa inicia-se com o estudo do tema da Trigonometria, em particular, com o estudo das Leis dos Senos e dos Co-senos, uma novidade em relação ao programa anterior. Como tal, estas duas leis são amplamente utilizadas nos vários problemas que envolvem a determinação das medidas dos lados e dos ângulos internos de vários polígonos, nomeadamente triângulos, e que são característicos do início do estudo deste tema.
No último artigo, escrevi sobre a Lei dos Senos e sobre a forma como ela pode ajudar na resolução de vários problemas. Poderia tê-lo feito também em relação à Lei dos Co-senos. De facto, tanto uma como a outra podem simplificar algumas resoluções, mas no entanto, nem sempre é assim. Por vezes, basta relembrar os conteúdos de base da Trigonometria e da Geometria para resolver alguns destes problemas de uma maneira mais simples.
O que vou descrever passou-se numa das minhas explicações.
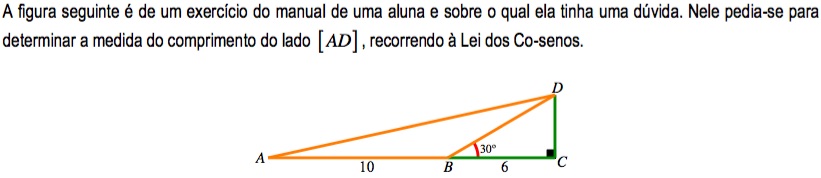
Começou por determinar a amplitude do ângulo BDC :
e em seguida utilizou a Lei dos Senos para determinar
![]()

Finalmente recorreu à Lei dos Co-senos para determinar
![]()
tendo em conta que
![]()
e fez todos os cálculos até chegar a
![]()
de onde concluiu que
![]()
Não gosto de “obrigar” os alunos a resolver um exercício ou um problema por um determinado método ou a seguir um caminho pré-definido, prefiro dar a liberdade ao aluno para fazer a resolução que entender. Apesar disso, perguntei-lhe se era possível resolver o exercício sem usar nenhuma das duas leis, isto é, “obrigando-a” a usar um outro método. Olhou para o exercício, pensou durante algum tempo e respondeu que não, ou melhor, que não estava a ver possibilidade de não as aplicar.
Perguntei-lhe então se era possível determinar
![]()
com a premissa estabelecida. Depois de algumas dicas lá percebeu como se poderia fazer:
![]()
Depois bastou fazê-la reparar que o triângulo [ACD] é rectângulo em C para se lembrar do mais famoso teorema da Matemática, o de Pitágoras, pelo que a conclusão do exercício foi imediata:
![]()
pelo que
![]()
No final alertei-a que devemos ter sempre em conta todas as ferramentas à nossa disposição. Às vezes percorrer um caminho, por mais óbvio que seja e por mais fácil que pareça, nem sempre é a melhor opção.
Nestas duas primeiras semanas de aulas tenho tido a sensação que pelo menos esta parte da Trigonometria passou a resumir-se às Lei dos Senos e dos Co-senos e que o resto, o que está na base, ficou esquecido. Do que tenho observado, os alunos têm escolhido, invariavelmente, caminhos que levam à aplicação destas leis. É verdade que são muito úteis, mas há vida na Trigonometria para além delas. Alertemos os nossos alunos para isso!
Deixe o seu o comentário sobre este artigo na página do Facebook do Clube SPM.


