(U)Ma Temática Elementar por José C. Santos
Eixos de Opinião março de 2014
|
|
José Carlos Santos - Departamento de Matemática da FCUP Dia 21 de cada mês
|
Artigo José Carlos Santos em (U)Ma Temática Elementar
Artigo de março de 2014
Clube de Matemática SPM
Facebook Clube SPMTítulo: Cuidado com as generalizações!
Considere-se o seguinte problema: marcam-se alguns pontos numa circunferência e unem-se todos os pares de pontos por segmentos de recta. Em quantas regiões é que o círculo delimitado pela circunferência fica dividido? Comecemos por um único ponto:
Neste caso há um só ponto e o círculo está dividido numa só região. E com dois pontos? Tem-se:
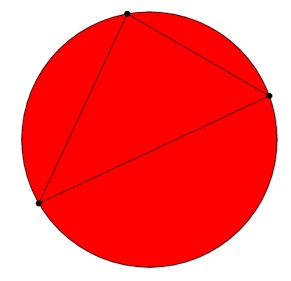
Ou seja, quando há dois pontos temos duas regiões. É fácil prosseguir esta contagem. Com três pontos temos:
Logo, no caso de haver três pontos, temos quatro regiões. É simples fazer isto, não é verdade. E quem tiver a curiosidade de prosseguir deste modo obterá que partindo de quatro pontos temos oito regiões e que partindo de cinco pontos temos dezasseis regiões. Há aqui um padrão não é verdade?
• um ponto — uma região;
• dois pontos — duas regiões;
• três pontos — quatro regiões;
• quatro pontos — oito regiões;
• cinco pontos — dezasseis regiões.
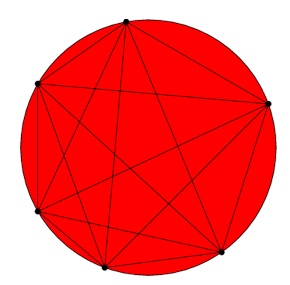
O padrão que parece emergir é este: se houver n pontos, haverá 2n – 1 regiões. Só que isto não é verdade! É que caso se usem seis pontos, então o círculo fica dividido em trinta e uma regiões e não em trinta e duas. Quem duvida, pode contá-las:
Isto é uma manifestação de um fenómeno que ocorre repetidamente na Matemática: ao estudar-se um padrão é frequente surgirem regularidades iniciais que não têm qualquer significado a longo prazo.
Um exemplo famoso deve-se a Fermat que, no século XVII, apercebeu-se de que os cinco primeiros números da forma 2n + 1 onde n é uma potência de 2 (podendo-se ter n = 1 = 20) são todos primos. Estes números (que hoje se designam por primos de Fermat) são 3, 5, 17, 257 e 65537. Fermat convenceu-se de que tinha provado de que este padrão se mantém, ou seja, que, sempre que n é uma potência de 2, 2n + 1 é primo. Mas no século seguinte, Euler provou que isto falha quando n = 26. De facto, nunca mais foi descoberto nenhum primo de Fermat e sabe-se que se n for um dos números 26, 27 e assim sucessivamente até 232, então 2n + 1 é composto.
O próprio Euler criou outro exemplo deste fenómeno, ao observar que os números da forma n2 + n + 41 são primos para n = 0, 1, 2, … Será que são todos primos? Sim se n for menor que 41, mas é claro que, para n = 41, n2 + n + 41 é simultaneamente um múltiplo de 41 e maior do que 41, pelo que é composto.
Sendo assim, um conselho ao leitor é aquele que vem no título do texto: cuidado com as generalizações!