Teoria dos Jogos por Alda Carvalho - Jogos incomparáveis em Teoria de Jogos Combinatórios
Eixos de Opinião de Julho de 2021

Alda Carvalho - Docente do Ensino Superior e Investigadora do CEMAPRE/ISEG. (Ver +)
Título: Jogos incomparáveis em Teoria de Jogos Combinatórios
Neste texto, respondendo à questão lançada no mês passado (Junho 2021) vamos apresentar o que são jogos incomparáveis.
No jogo DOMINÓRIO, alternadamente, cada jogador coloca uma peça de dominó sobre 2 quadrados vazios. O primeiro jogador (bLue ou verticaL) só pode colocar as suas peças na vertical e o segundo jogador (Red ou hoRizontal) só pode colocar as suas peças na horizontal. O jogo acaba quando um dos jogadores não consegue jogar e, quando isso acontece, esse jogador perde o jogo.
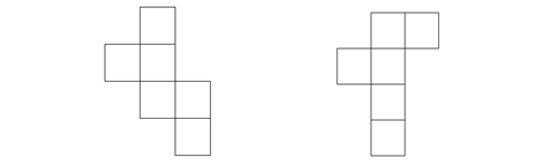
Será que algum dos jogadores (verticaL, hoRizontal) prefere alguma destas componentes?
Se as componentes forem jogadas isoladamente, jogando em segundo lugar, o jogador verticaL ganha a componente da esquerda e perde a da direita.
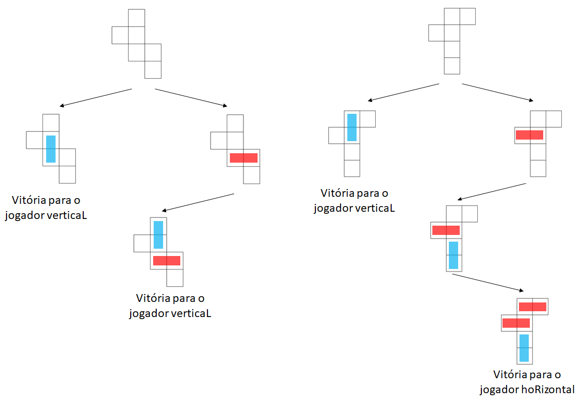
Portanto, nessa circunstância, o jogador verticaL prefere a componente da esquerda. No entanto, quando se pretende compreender um jogo na sua globalidade, não basta analisar as componentes de forma individual, é preciso perceber como se comportam «em grupo».
Por exemplo, analisando as componentes anteriores com a presença de um «pequeno L», jogando em segundo lugar, o jogador verticaL ganha a componente da direita e perde a componente da esquerda.
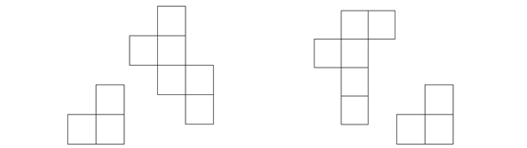
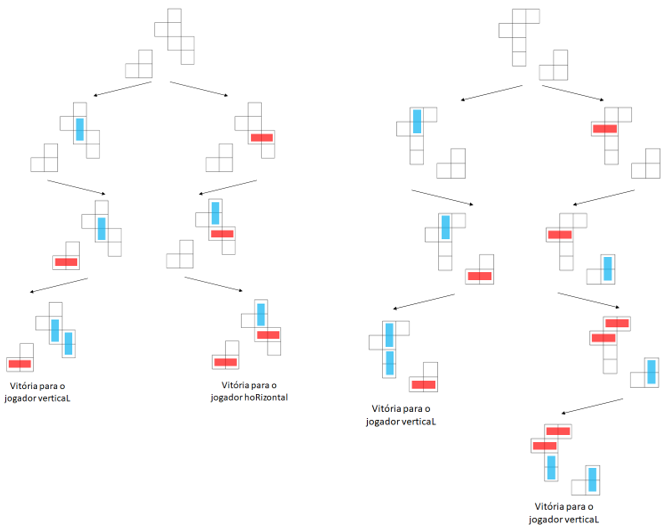
Portanto, nessa circunstância, o jogador verticaL prefere a componente da direita. Sendo assim, dados dois jogos G e H, não é obrigatório ter-se G maior ou igual a H ou H maior ou igual a G. Quando não se tem nem uma coisa nem outra, os jogos dizem-se incomparáveis e escreve-se G||H.
Quando dois jogos G e H são incomparáveis, isso significa que há circunstâncias em que se prefere G e outras circunstâncias em que se prefere H. É por isso que, ao contrário do que acontece com os números reais, a ordem dos jogos combinatórios não é total, mas sim parcial. Voltaremos a este assunto em Setembro, boas férias!

