Incógnitas Matemáticas/Ciências - O problema do Caixeiro Viajante
Problema do caixeiro-viajante
Definição e formulação do problema
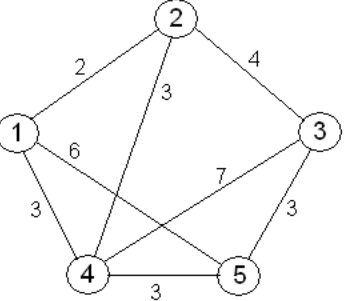
O problema do caixeiro-viajante (representado na Figura 1) consiste na procura de um circuito que possua a menor distância, começando numa qualquer cidade, entre várias, visitando cada cidade precisamente uma vez e regressando à cidade inicial (Nilsson, 1982).
A origem do nome «travelling salesman problem» é desconhecida. Não parece existir qualquer documento que prove o(a) autor(a) do nome do problema. Merril Flood, da Universidade de Princeton, um dos investigadores mais proeminentes nas primeiras aplicações do problema proferiu, no entanto, o seguinte comentário: «I don´t know who coined the peppier name "Traveling Salesman Problem" for Whitney's problem, [...]» (Applegate et al., cop. 2006, p. 2).
Nos anos de 1800, problemas relacionados com o PCV começaram a ser desenvolvidos por dois matemáticos: o escocês William Rowan Hamilton e o britânico Thomas Penyngton Kerkman. A forma geral do PCV parece ter sido, pela primeira vez, estudada por matemáticos nos anos de 1930 em Harvard e Viena. O problema foi posteriormente estudado por Hassler Whitney e Merril Flood em Princeton. Exceptuando pequenas variações ortográficas, como traveling vs travelling ou salesman vs salesman's, o nome do problema ficou globalmente conhecido por volta do ano 1950 (Applegate et al., cop. 2006, p.2).
O problema do caixeiro-viajante (PCV), travelling salesman problem (TSP) (em inglês) , é um problema de optimização que, apesar de parecer modesto é, na realidade, muito investigado por cientistas, matemáticos e investigadores de diversas áreas, tais como: logística, genética e produção, entre outros (Applegate et al., cop. 2006, p. 1).
E, para já é um problema sem solução à vista. A Matemática também tem problemas...sem solução.
Incógnitas - Curiosidades sobre o mundo científico/matemático

Nesta rubrica vão aparecer pequenas curiosidades do mundo científico/matemático:

